Диаграмма Эйлера: где применяется и как построить

Что это такое? Диаграмма Эйлера кажется чем-то очень сложным на первый взгляд. Однако на самом деле это круги, накладываемые друг на друга при решение определенных задач. Их применяют в алгебре, информатике и даже в жизни, столкнувшись с каким-то выбором.

Как строить? Для начала нужно представить универсальное множество в виде прямоугольника. Внутри него будут эллипсы или круги, которые могут пересекаться, а могут и нет. Их можно дополнять, объединять, пересекать. Давайте рассмотрим все это на примере ниже.

Что собой представляет диаграмма Эйлера

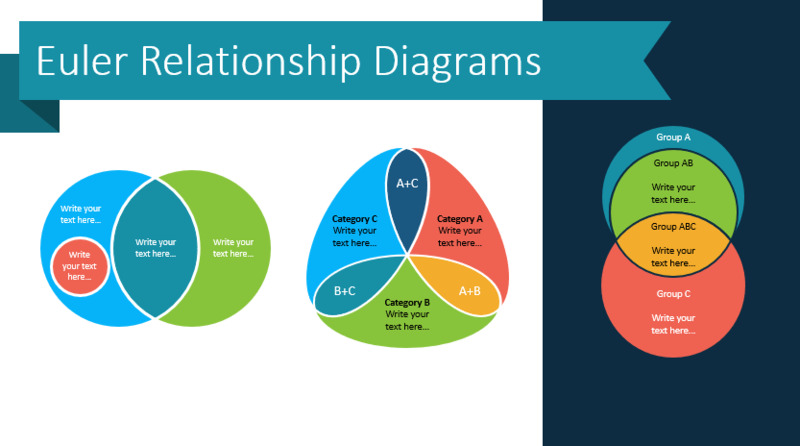
Так называется геометрическое изображение, которое используют, чтобы смоделировать множества и схематично отразить отношения между ними. На диаграмме Эйлера наглядно показаны утверждения о данных множествах.

При этом универсальное множество обозначено прямоугольником, а подмножества изображены в виде кругов. Поэтому диаграмму называют также «круги Эйлера». Такое схематичное изображение применяют при решении математических и логических задач, а также в менеджменте и различных прикладных целях.

Автор этого способа – математик XVIII века Леонард Эйлер, который хотел таким образом помочь размышлениям. Автором кругов является известный математик Леонард Эйлер, который считал, что они необходимы, чтобы облегчить размышления человека. Диаграмма Эйлера стала признанным методом с момента своего появления.

Узнай, какие ИТ - профессии
входят в ТОП-30 с доходом
от 210 000 ₽/мес

Павел Симонов

Исполнительный директор Geekbrains

Команда GeekBrains совместно с международными специалистами по развитию карьеры подготовили материалы, которые помогут вам начать путь к профессии мечты.

Подборка содержит только самые востребованные и высокооплачиваемые специальности и направления в IT-сфере. 86% наших учеников с помощью данных материалов определились с карьерной целью на ближайшее будущее!

Скачивайте и используйте уже сегодня:

Павел Симонов

Исполнительный директор Geekbrains

Топ-30 самых востребованных и высокооплачиваемых профессий 2023

Поможет разобраться в актуальной ситуации на рынке труда

Подборка 50+ бесплатных нейросетей для упрощения работы и увеличения заработка

Только проверенные нейросети с доступом из России и свободным использованием

ТОП-100 площадок для поиска работы от GeekBrains

Список проверенных ресурсов реальных вакансий с доходом от 210 000 ₽

Получить подборку бесплатно

pdf 3,7mb

doc 1,7mb

Уже скачали 31976

Биография Леонарда Эйлера связана со Швейцарией, Пруссией и Россией. Этот учёный оказал огромное влияние на развитие математики, механики, физики. Его научные работы (более 850 трудов) затрагивают теорию чисел, теорию музыки, оптику, баллистику, небесную механику. Среди его трудов имеется ряд основополагающих монографий. Около половины жизни Эйлер провёл в России, работал в Петербургской Академии наук и много вложил в развитие российской науки.

В дальнейшем в работах многих учёных используется диаграмма Эйлера для множеств: это математики Бернард Больцано и Эрнест Шредер; философ и логик Джон Венн и другие. В наши дни эту методику применяют для развития мышления как при очном обучении, так и на различных онлайн-курсах.

Разница между диаграммой Эйлера и диаграммой Эйлера-Венна

Диаграммы Эйлера-Венна – это частный случай кругов Эйлера, который показывает все 2^π{\displaystyle 2^{n}} комбинаций π{\displaystyle n} свойств, то есть конечную булеву алгебру. При π = 3 диаграмма Эйлера-Венна обычно выглядит как три круга, имеющих одинаковый радиус, их центры совпадают с вершинами равностороннего треугольника, стороне которого приблизительно равны радиусы.

Если определённая комбинация свойств соответствует пустому множеству, на схеме эту область закрашивают. Диаграммы Эйлера могут быть не типичны, а иногда эквивалентны диаграммам Венна. Закрашенный участок схемы указывает на то, что это множество не содержит элементов, то есть пустое.

Задачи, решаемые диаграммой Эйлера

Прикладное значение, которое имеет диаграмма Эйлера: задачи на соотношение множеств в математике, логике, информатике, статистике становятся понятнее при её использовании. Круги Эйлера можно применять и в жизни, находя с их помощью взаимосвязи и отвечая на возникающие насущные вопросы.

Круги Эйлера можно разделить на такие группы:

• равнозначные;
• пересекающиеся;
• подчиненные;
• соподчиненные;
• противоречащие;
• противоположные.

Читайте также!

Типы диаграмм и сервисы по их созданию

Подробнее

Выполняя упражнения на развитие мышления, чаще всего можно столкнуться с двумя их видами:

• Круги, изображающие объединяющиеся понятия и вложенные один в другой, чтобы это показать.
• Круги, иллюстрирующие пересечения различных множеств, которые имеют те или иные общие признаки.

Приведём пример использования кругов при выборе профессии. Можно перебирать варианты, обдумывая наиболее подходящий, а можно начертить схему, изобразив в виде кругов то, что вам нравится делать, что вы умеете, и что хорошо оплачивается. Получится диаграмма Эйлера. Пересечение этих трёх кругов и показывает, что будет наиболее вам подходить.

Принцип построения диаграммы

При построении диаграммы Эйлера сначала рисуют большой прямоугольник, обозначающий универсальное множество U. Внутри этого прямоугольника располагают фигуры, которые являются изображением множеств: круги (если их не больше трёх) или круги и эллипсы (когда множеств четыре и больше). Фигуры пересекаются различными способами, в зависимости от условий задачи.

Допустим, у нас имеется выражение А. Изображаем на диаграмме круг, обозначающий множество А. Пространство внутри круга показывает значения, при которых выражение А будет истинным, а область снаружи обозначает ложь. Чтобы отобразить на схеме логическую операцию, заштрихуем те части диаграммы, в которых значения истинны. В результате мы отмечаем область, где множества пересекаются.

Можно доказать любой закон алгебры, представив его в виде графической схемы при помощи диаграммы Эйлера. Алгоритм действий таков:

1. Сначала чертим диаграмму и заштриховываем все множества, которые находятся с левой стороны от знака «равно».
2. Затем нужно начертить другую диаграмму и на ней заштриховать множества, находящиеся справа от знака равенства.
3. Если на диаграммах окажется заштрихованной одна и та же область, тождество будет истинным.

Сильнее углубимся в тему.

Дополнение множества

Дополнением к множеству A будет множество Его элементы не относятся к множеству А.

= {x | x ∉ A}

Но в включаются не все элементы, не относящиеся к А. По условиям применения диаграммы Эйлера, все множества, о которых идёт речь в задаче, будут включены в универсальное множество U, то есть являются его подмножествами. С учётом этого дополнение будет определяться так:

=U∖A

Объединение множеств

Объединением двух множеств (назовём их А и В) будет множество A ∪ B, состоящее из элементов, которые включаются хотя бы в одно из них.

Это можно записать так:

A ∪ B={x |x ∈ A или x ∈ B}

Пересечение множеств

Пересечение множеств A и B это множество A ∩ B. Оно состоит из элементов, которые входят и в множество А, и в то же время в множество В.

Записывается пересечение множеств так:

A ∩ B = {x | x ∈ A и x ∈ B}

Симметричная разность множеств

Симметричная разность – это множество A \ B, в которое включаются элементы, которые входят только в одно из множеств А и В, но не в оба сразу.

Запись симметричной разности выглядит таким образом:

A △ B = (A ∖ B) ∪ (B ∖ A)

Разность множеств

Разностью A \ B являются элементы множества A, не входящие в B.

Записанная разность множеств выглядит так:

A ∖ B = {x | x ∈ A и x ∉ B}

Только до 25.11

Скачай подборку материалов, чтобы гарантированно найти работу в IT за 14 дней

Список документов:

ТОП-100 площадок для поиска работы от GeekBrains

20 профессий 2023 года, с доходом от 150 000 рублей

Чек-лист «Как успешно пройти собеседование»

Чтобы получить файл, укажите e-mail:

Введите e-mail, чтобы получить доступ к документам

Подтвердите, что вы не робот,
указав номер телефона:

Введите телефон, чтобы получить доступ к документам

Скачать подборку бесплатно pdf 2,5mb

Уже скачали 52300

Я подтверждаю согласие на обработку персональных данных.

Применение диаграмм для доказательства логических равенств

Давайте рассмотрим, как применяется диаграмма Эйлера на примере доказательства логического равенства.

Представим, что мы имеем конъюнкцию множеств A ∧ B.

Сначала работаем с левой частью равенства. Нужно с помощью диаграммы Эйлера построить множества А и В, заштриховать оба круга цветом и таким образом выделим дизъюнкцию.

Дальше нужно показать инверсию с помощью штриховки области за пределами этих множеств.

Теперь переключаемся на правую часть равенства. Сперва показываем цветной штриховкой за пределами круга А инверсию этого множества.

То же самое действие выполняем для множества В.

Штрихуем чёрным цветом все области пересечения и получаем графическое отображение конъюкции инверсий множеств А и В.

Сравнивая области, отображающие правую и левую части равенства, убеждаемся, что они равны. Таким образом, истинность логического равенства доказана при помощи диаграммы Эйлера.

Пример решения задачи с помощью кругов Эйлера

В демонстрационном тесте ЕГЭ по информатике и ИКТ была представлена задача, которую мы решим с применением этого метода.

Условия задачи:

В языке запросов поискового применяется символ «|» для логической операции «или» и символ «&», чтобы обозначить логическую операцию «и».

Таблица, приведённая ниже, отражает запросы в некотором сегменте сети Интернет и количество найденных страниц по этим запросам.

Вопрос: какое количество страниц (в тысячах) найдётся, если запрос будет сформулирован в виде Крейсер & Линкор?

Принимаем версию, что все запросы выполняются в один отрезок времени, поэтому набор страниц, которые включают искомые слова, остался неизменным.

Решение:

Покажем условие задачи при помощи диаграммы Эйлера. Используем цифры 1, 2 и 3 для обозначения полученных областей.

Читайте также!

Столбчатые диаграммы: виды, сферы применения

Подробнее

Используя условия задачи, составляем уравнения:

1. Крейсер | Линкор: 1 + 2 + 3 = 7000
2. Крейсер: 1 + 2 = 4800
3. Линкор: 2 + 3 = 4500

Искомая область Крейсер & Линкор обозначенная на чертеже цифрой 2, находится путём подстановки уравнения (2) в уравнение (1). Получаем следующее:

4800 + 3 = 7000, откуда получаем область 3, равную 2200.

Полученный результат мы подставляем в уравнение (3). Получаем результат:

Область 2 + 2200 = 4500, значит, она равна 2300.

Ответ: будет найдено 2300 страниц по запросу Крейсер & Линкор.

Этот пример показывает, что можно решать с помощью диаграммы Эйлера задачи, являющиеся достаточно сложными или запутанными.

Дарим скидку от 60%
на курсы от GeekBrains до 01 декабря

Уже через 9 месяцев сможете устроиться на работу с доходом от 150 000 рублей

Забронировать скидку

Можно сделать вывод, что круги Эйлера не просто занимательный, но и полезный в плане решения учебных и бытовых задач метод. Многие вещи можно представить в виде множеств, а поможет наглядно представить их пересечение или объединение диаграмма Эйлера.

Советуем применять этот метод для решения задач и непременно поделитесь этим полезным и наглядным способом с друзьями.

Автор статьи:

Редакция сайта GeekBrains Шеф-редактор раздела Программирование