Получите новые возможности став разработчиком
Удаленная работа и гибкий график — можно жить в Тайланде, а работать на компанию в Москве
Быстрый рост дохода — зарабатывать от 100 000 ₽ можно с опытом 1–2 года
Ваша зарплата будет расти вместе с опытом
~ 70 000 ₽
Junior, после курса
~ 120 000 ₽
Middle, с опытом от 1 до 3 лет
~ 200 000 ₽ и больше
Senior, с опытом от 3 лет
Источник: HeadHunter
Нейросети — новая норма, и мы поможем к ней адаптироваться
Больше 70% россйиских ИТ‑специалистов используют ИИ в работе
На бонусном курсе «AI‑помощники для IT‑специалистов: ChatGPT и аналоги» вы узнаете, как с помощью нейросети писать код и проверять его на ошибки. Автоматизируете большую часть рутины и ускорите свою работу.

Курс подойдет каждому

Тому, кто не знает, какую профессию выбрать в IT

Тому, кто ничего не знает о разработке, и хочет начать с азов

Тому, кто выбрал профессию, но не уверен до конца
Создали один курс, чтобы вы точно стали разработчиком
Какие профессии будут доступны на выбор
Ваши будущие проекты
Как проходит обучение
Преподаватели — лидеры IT отрасли
Мы помогаем с трудоустройством
Карьерные специалисты будут помогать вами до тех пор, пока вы не получите работу
Проведем тестовые собеседования, подготовим к реальным интервью — сделаем так, чтобы вы точно получили офер
Программа обучения
Актуальна на 2024 год
Трудоустройство
Задания и проекты
Начало
Профориентационный тест
Пройдете тест и получите ответ, какая профессия вам подходит
- Наш профориентационный тест старается учитывать ваши личные особенности, текущие навыки, прошлый опыт, желания, интересы и другие параметры вашей личности. Поэтому подборка профессий, которые вы получите после прохождения теста, будут вам максимально близки по духу.
Знакомство с профессиями
Поймете особенности современных профессий и попробуете их на практике
- После профтеста вы сможете подробнее узнать про те профессии, которые больше всего вам подходят. Для каждой профессии подготовлен интерактивный рассказ в виде статей с видео, тестами и опытом экспертов. Про каждую профессию вы узнаете: чем занимаются специалисты, сколько можно заработать, где и как искать работу + решите несколько задач, чтобы вы могли «примерить» профессию.
Выбор профессии для дальнейшего изучения
Вы прошли тест, изучили материалы и готовы осознанно подойдете к выбору профессии
- На выбор доступны основные профессии: Python-разработчик, Frontend-разработчик, Java-разработчик, 1С-разработчик, разработчик игр, менеджер проектов и продакт-менеджер.
- Также на выбор доступны дополнительные профессии из других направлений: аналитика, дизайн, маркетинг, кино, музыка и игры — на тот случай, если помимо IT вам понравится что-то другое.
Профессии на выбор
Python-разработчик
78 практических заданий, 3 проекта
- Ваши инструменты: Python, PyCharm, GitLab, SQL, MySQL, PostgreSQL, Docker, Flask, FastAPI, HTML, CSS
- Научитесь работать с базовыми алгоритмами и типами данных в Python, понимать принципы ООП, работать с системами очередей задач
- Получите опыт работы с фреймворками Django, Flask и FastAPI, научитесь автоматизации развертывания приложений с Docker и работать с базами данных и API
- Узнаете принципы работы протоколов HTTP, HTTPS и WebSockets, сможете использовать систему контроля версий Git и настраивать CI/CD в GitLab
Frontend-разработчик
115 практических заданий, 9 проектов
- Ваши инструменты: Chrome DevTools, CSS, Element Plus, Emmet, Eslint, Figma, GitHub, GitLab, HTML, JavaScript, Jest, Lighthouse, Pinia, Pixel Perfect, React, REST API, Sass, TypeScript, Vite, Vitest, VS Code, Vue 3.0, Webpack
- Научитесь адаптивной верстке на HTML/CSS, разрабатывать интерактивные элементы на JavaScript, работать с промисами, хранилищем данных и Cookie
- Сможете программировать на TypeScript, React.js и Vue.js, работать со сборщиками Webpack, Vite, научитесь командной разработке в Git
- Получите опыт работы с дизайн-макетами в Figma, кросс-браузерной и адаптивной версткой, научитесь оптимизировать страницы, писать тесты на Jest и Vitest
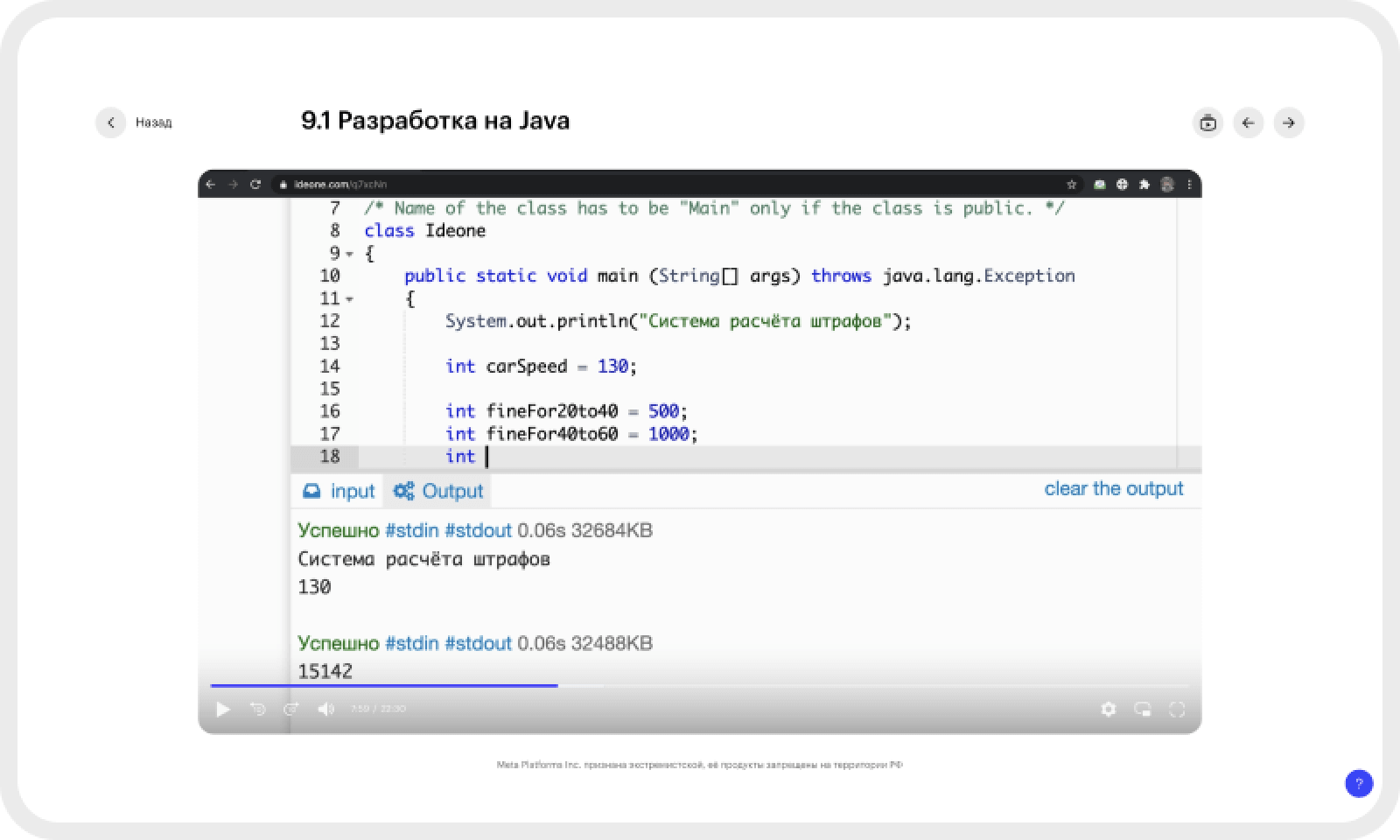
Java-разработчик
60 практических заданий, 5 проектов
- Ваши инструменты: CSS, Docker, Entity Framework, GitLab, HTML, IntelliJ idea, JUnit, Maven, MongoDB, MySQL, Redis, Spring, Spring Boot
- Научитесь разработке веб-приложений на Java, применять паттерны проектирования приложений, поймете принципы объектно-ориентированного программирования
- Сможете применять алгоритмы для решения разных задач, тестировать приложения, работа с системой контроля версий Git
- Получите опыт разработки многопоточных приложения, научитесь работать с нереляционными базами данных (Redis, MongoDB), получите навыки интеграции с внешними системами (Rest, Kafka)
1С-разработчик
20 практических заданий, 17 проектов
- Ваши инструменты: 1C:Предприятие 8.3, Конструктор запроса, Конфигуратор, СКД, HTTP, SQL, XML,
- Научитесь работать с оперативным и бухгалтерским учетом, составлять технические задания, управлять совещаниями, дорабатывать типовые конфигурации
- Сможете разрабатывать внешние отчеты, обработки и печатные формы, научитесь разрабатывать подсистемы периодических расчетов, интегрировать 1С с другими системами, работать с SQL и администрированием баз данных
Разработчик игр (Unity или Unreal Engine)
80+ практических заданий, 10+ проектов
- Ваши инструменты: Unreal Engine, C++, GitLab, Unity, Visual Studio, Blender
- Разработка игр для ПК, Android и iOS, программирование на C++ и визуальный скриптинг на Blueprints, применение принципов ООП и паттернов проектирования в геймдеве, знание идиом C++ и библиотеки STL
- Написание автотестов на C++, создание плагинов для Unreal Engine Editor, работа с resharper для рефакторинга и статического анализа, навыки многопоточной разработки
- Разработка 2D- и 3D-игр на Unity, разработка и адаптация игр под ПК, iOS, Android, создание 3D-моделей в Blender, оптимизация игровых проектов для разных платформ, разработка шейдеров, интеграция SDK и плагинов в Unity 3D-проекты, работа с Git (локальные и удаленные репозитории)
Менеджер проектов
60+ практических заданий, 9 проектов
- Ваши инструменты: Google Docs, Google Slides, Google Sheets, Яндекс Метрика, Lean Canvas, Miro, RACI, Customer persona, Excel
- Ведение переговоров с заказчиками, разработка концепции и жизненного цикла проекта, управление командой по Agile и Scrum
- Планирование работы и оценка задач, оценка рисков и стратегическое планирование, формирование команды под проект
- Понимание инструментов продвижения, презентация проектов и результатов
Продакт-менеджер
30+ практических заданий, 3 проекта
- Ваши инструменты: AppMetrica, Яндекс Метрика, Miro, Tilda, Figma, Power BI, CJM, CustDev, SQL, Excel
- Анализ рынка и конкурентов, проработка монетизации продукта, просчет юнит-экономики, анализ пользователя, управление командой разработки
- Анализ продуктовых метрик, разработка стратегии развития продукта, создание MVP продукта, презентация идей и результатов
- Тестирование гипотез, визуализация и презентация данных
Другие профессии
Более 20 профессий дополнительно доступно на выбор
- Если захотите, вместо профессий в разработке можно выбрать профессии из других направлений: маркетинг, дизайн, игры, кино и музыка
Трудоустройство
Трудоустройство по итогу обучения
Поможем найти работу или вернем деньги за обучение
- Вас ждет индивидуальная поддержка HR-специалиста. Вместе вы составите резюме, подготовите портфолио и разработаете карьерный план, который поможет найти работу быстрее. Сможете выбрать привлекательные вакансии партнеров и получите приоритет перед другими соискателями.
Вы получите сертификат и подтвердите, что стали разработчиком
Официальный сертификат повысит ваши шансы на трудоустройство среди других кандидатов

Подтвердим
вашу квалификацию
вашу квалификацию
В конце обучения вы сможете получить удостоверение о повышении квалификации установленного образца. Мы обучаем по государственной лицензии № Л035−1 298−77/179 609.

Поможем дойти до конца обучения

Куратор-эксперт
Подробно разбирает домашние задания, помогает сделать их лучше

HR-консультант
Помогает в поиске работы: от плана действий до собеседований

Служба заботы
Помогает с вопросами по платформе и прохождению курса
Выгодные условия оплаты
Рассрочка под 0%,
без переплаты и скрытых платежей
без переплаты и скрытых платежей
Без первого взноса
Можно вернуть до 13%
от цены курса
от цены курса
Воспользуйтесь налоговым вычетом
Стоимость курса
9 176 ₽/мес.
4 588 ₽/мес.
В рассрочку на 36 месяцев.
-50%
До конца действия скидки осталось
12
20
10
50
Указана стоимость базового тарифа. Больше практики и поддержки в продвинутых тарифах.
Часто задаваемые вопросы
Почему этот курс идеальный старт для новичков в IT? Как устроен курс?

Сколько по времени нужно учиться?

Получится ли совмещать обучение с другими делами? Сколько часов в неделю надо уделять обучению?

Если я никогда не занимался разработкой, не знаю математику и английский язык, я смогу обучаться на курсе?

А если мне не подойдет разработка, что тогда?

Как можно оплатить обучение?

Действительно ли вы помогаете с трудоустройством?

Что значит совместная программа?