Наследие Тьюринга: машина, тест и полнота
Если вы не учились профессии программиста в вузе или не ходили в специальную школу, то, возможно «Машина Тьюринга» для вас просто дешифратор из курса истории или фильма «Игра в имитацию». В действительности всё немного сложнее, любому уважающему себя программисту необходимо знать и понимать, что это такое.

Что такое машина Тьюринга
Для того, чтобы представить простейшую машину Тьюринга, взглянем на её художественную реализацию:
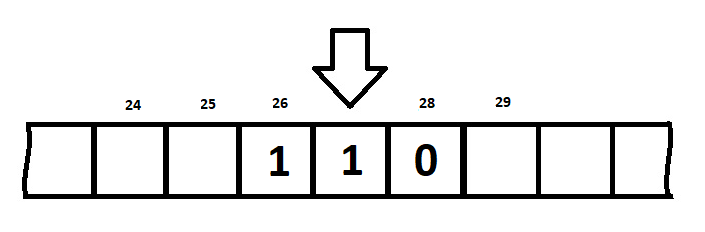
Это бесконечная лента, не имеющая ни начала, ни конца, поделённая на ячейки. Для работы с ней мы используем некое управляющее устройство (автомат), для визуализации выбрана каретка. В каждый момент времени она имеет состояние qj и считывает содержимое ячейки ai. О том, что происходит в остальной части ленты, каретка не знает, соответственно оперировать она может только текущими данными. Всего возможно три типа действий, зависящий от этой композиции:
- выполнить сдвиг на соседнюю ячейку;
- записать в текущую новое содержимое;
- изменить состояния.
Что-то похожее реализовано в электронных таблицах: там тоже условно неограниченное поле, вы можете изменить значение ячейки, изменить действие или перейти на другую ячейку.
Множества A = {a0, a1, ..., ai} и Q = {q0, q1, ..., qj} являются конечными, a0 – символ пустой ячейки, q1 – начальное состояние, q0 – пассивное состояния, условие выхода машины из цикла.
Создадим таблицу для реализации алгоритма Тьюринга:

Символами _Л, _П, _Н обозначим направление движения автомата – соответственно сдвиг «влево», «вправо» или неподвижное положение.
Пусть наша лента выглядит так:
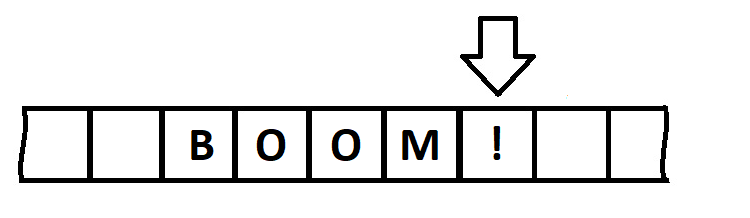
Начальное положение – крайняя правая ячейка, остановка – в пустой клетке. Догадались как она будет выглядеть после завершения алгоритма?
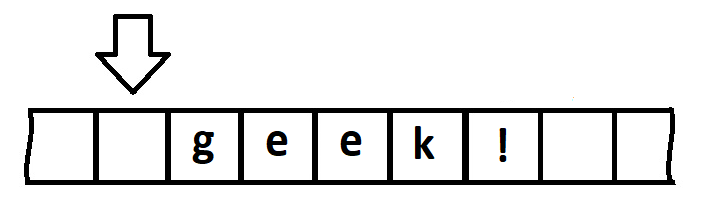
На указанном примере всё выглядит довольно просто. Можете поиграть с увеличением алфавита, преобразованием состояний, помещением начальной позиции не в крайнюю позиции, условиями выхода из цикла и т.д. Фактически, практически любую задачу преобразования можно решить с помощью машины Тьюринга.
Зачем это программисту
Машина Тьюринга позволяет размять мозги и взглянуть на решение задачи иначе. В конечном счёте, с той же целью следует познакомиться с:
- нормальным алгоритмом Маркова;
- лямбда-вычислениями;
- языком программирования Brainfuck.
Но машина Тьюринга – базовая теория алгоритмов, которая помогает думать не столько о средствах языка, сколько о различных путях решения задачи. Для профессионального роста – это необходимый навык.
Полнота по Тьюрингу
Ещё один важный вопрос, связанный с именем известного математика. На форумах и в статьях вы неоднократно могли видеть выражение «полный\не полный язык программирования по Тьюрингу». Ответ на вопрос «что это означает?» возвращает нас к описанной выше теории. Как уже было сказано, машина Тьюринга позволяет выполнить любое преобразование, соответственно, вы можете реализовать на ней абсолютно любой алгоритм или функцию. То же самое относится и к языкам. Если с его помощью вы можете реализовать любой заданный алгоритм – он тьюринг-полный. Если в дело вступают ограничения синтаксиса или любые физические – не полный.
Тест по Тьюрингу
Последний раздел никак не связан с машиной. Тест Тьюринга – игра, в ходе которой человек с помощью текстовых сообщений взаимодействует одновременно с машиной и другим человеком, не видя их. Задача машины – ввести участника в заблуждение.
Такой тест на долгие годы предопределил развитие ИИ – программы вроде Элизы или PARRY строились именно на копировании человеческого поведения машиной. Уже позднее, когда стало понятно, что путь тупиковый, вектор развития был сдвинут в сторону изучения механизмов интеллекта. Однако до сих пор тема «способна ли мыслить машина» лежит в основе многих тестов, романов и кинофильмов.
Алан Тьюринг остался в истории не только человеком, совершившим важное открытие во время Второй мировой войны, но и подаривший миру несколько фундаментальных теорий, которыми пользуется человечество до сих пор.
